Рассмотрена вероятностная модель оценки погрешности определения координат источников акустической эмиссии (АЭ) на основании экспериментальных данных. Для получения большого числа сигналов АЭ в объект контроля вдавливали шарообразный индентор. Обработка параметров сигналов позволила выявить зависимость вероятности определения координаты с заданной точностью от максимальной амплитуды! и времени нарастания сигналов АЭ. Также рассмотрена возможность выбора способа определения времен прихода сигналов АЭ на приемники в зависимости от параметров сигнала.
Ключевые слова: акустическая эмиссия, амплитуда, вероятность, время нарастания, время прихода, определение координат, погрешность, порог, сигнал.
Одним из важнейших этапов при использовании акустико-эмиссионного метода диагностики является определение координат источников. Эта задача актуальна как для источников дискретной, так и непрерывной АЭ. Как правило, методики определения координат встроены в программное обеспечение обработки и представляют собой аналитическое решение или зонную локацию [1, 2] с учетом акустических характеристик материала и параметров пьезоантенны.
Однако при решении задачи локации источников практически не учитываются особенности акустического тракта в материале, т.к. для большинства сосудов и аппаратов большого различия в его акустических свойствах и параметрах не наблюдается. В то же время активное развитие акустикоэмиссионного метода для контроля деталей и конструкций более сложной формы (таких как мостовые конструкции, детали подвижного состава, объемные объекты) показывает, что в этом случае погрешности определения координат источников существенно возрастают [2—4]. В связи с этим использование простых методик локации источников сопряжено с достаточно большими погрешностями оценки координат и, таким образом, снижает достоверность акустико-эмиссионного контроля.
Данная работа посвящена анализу точности локации источников АЭ на литых деталях, контролируемых акустико-эмиссионным методом при продлении ресурса. Учитывая решающую роль локации источников в определении активных источников в таких деталях, решение этой задачи непосредственно влияет на надежность метода при продлении ресурса литых деталей подвижного состава.
При определении координат источника АЭ аналитически решается система квадратных уравнений, где используются задаваемые параметры (координаты приемных преобразователей, скорость распространения ультразвуковой волны и разности времен прихода на приемники, определяемые при распознавании сигналов). Следует отметить, что для метода АЭ целесообразно использовать не скорость ультразвуковой волны, а скорость волнового пакета, состоящего из нескольких типов волн, порожденных источником и формой объекта контроля на пути акустического тракта. Так, согласно [5], любое продвижение трещины в объемном материале является источником как продольных, так и поперечных волн, которые в зависимости от толщины и взаимодействия с границами могут трансформироваться друг в друга и другие типы в зависимости от конфигурации объекта. Поэтому для определения координат источников регистрируется время прихода сигнала на каждый приемный преобразователь.
Предварительные прямые измерения скорости распространения волны на литых деталях с известными координатами источника относительно приемных преобразователей показали, что значение скорости ввиду того, что сигнал является суперпозицией различных типов волн, генерируемых источником, колеблется в диапазоне 2300 — 5850 м/с [6]. В качестве источника использовали имитатор Су-Нильсена и вдавливание стального индентора в виде шарика диаметром 4 мм. Именно разброс этих данных может иллюстрировать погрешность, вносимую искажениями акустического тракта.
Приведенные обстоятельства заставляют искать в объектах сложной формы другие способы повышения достоверности определения координат, в частности было предложено использовать собственные параметры сигналов АЭ и их статистическую оценку. Для этого проведены эксперименты по созданию большого потока сигналов АЭ из источника на участке литой детали, на
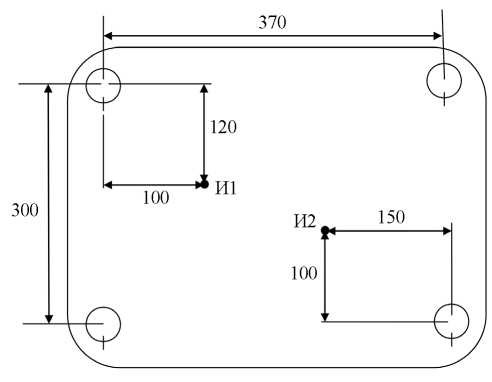
Рис. 1. Схема расположения приемников и источника АЭ на участке надрессорной балки при оценке погрешности определения координат источника.
со сторонами 370 и 300 мм, а внутри нее — источники — деформирующиеся области под воздействием шарообразного индентора диаметром 5 мм, вдавливаемого в поверхность детали силой 630 кН. Индентором воздействовали сначала в точке И1, а затем в точке И2 (рис. 1). Порог чувствительности каналов составил 30 мкВ, при регистрации соответствующего сигналу электронного имитатора — 30 мВ. Регистрировали и обрабатывали все сигналы АЭ, превышающие порог чувствительности.
В экспериментальной части работы поток сигналов АЭ был обеспечен вдавливанием шарообразного индентора диаметром 5 мм. Такой имитатор имеет важное преимущество перед другими источниками, так как деформирование материала в месте вдавливания сопровождается сложными и разнообразными механическими процессами: перемещениями дислокаций, образованием микротрещин, расслоений, наклепом металла и т.п. Все эти процессы порождают различного типа и направления акустические поля и волны, что приводит к регистрации сигналов от источника с низким коэффициентом корреляции, то есть разной формы и величины. Обработка таких сигналов формирует наибольшее разнообразие волновых пакетов сигналов АЭ от источника, реальные координаты которых находятся в ограниченном объеме.
При испытаниях первого индентора число локализованных сигналов составило 790, при вдавливании второго — 306. Все сигналы имеют экспоненциально убывающее по амплитуде распределение для обоих опытов. Активность источника на всем протяжении каждого опыта изменялась слабо и была на уровне 60 сигн/с. Нагружение проводили в каждом опыте в течение 120 с.
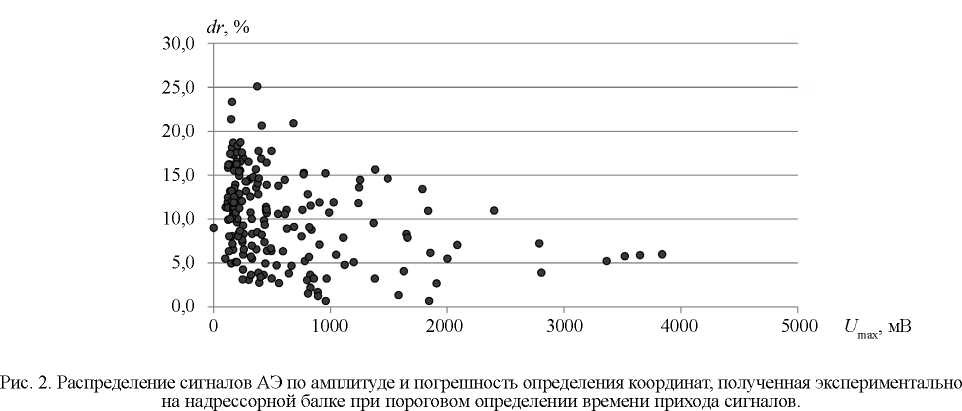
Общая картина распределения сигналов по амплитуде и погрешности определения координат каждого зарегистрированного сигнала приведена на рис. 2, где,. — максимальная амплитуда сигнала, зафиксированная ближайшим к источнику приемником;
— относительная к размеру стороны прямоугольной пьезоантенны погрешность определения координат. При этом погрешность определения координат
вычисляли по формуле
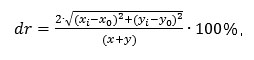
где х. и у. — координаты источника, вычисленные для 7-го сигнала аналитическим путем [7] с учетом времен прихода, определенных одним из используемых способов; х0 и у0 — истинные координаты источника АЭ; х и у — размеры сторон прямоугольной пьезоантенны.
Видно, что сигналы с малой максимальной амплитудой относительно порога имеют существенно больший разброс погрешности оценки координат, кроме того, для половины из них недостаточно данных для определения координат. В то же время повышение уровня амплитуд приводит к постепенному снижению разброса погрешностей и самой погрешности определения координат. Однако если представить полученные результаты в виде распределения вероятности определения координат с погрешностью
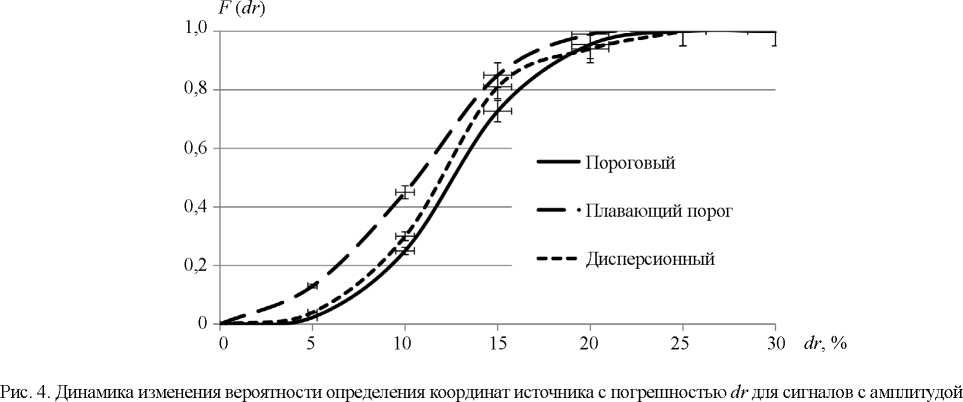
в зависимости от основных параметров — максимальной амплитуды сигнала и времени его нарастания, пришедшего на ближайший к источнику приемник, то они будут выглядеть так, как показано на рис. 3. Видно, что они отражают фиксацию времен прихода сигнала на каналы пороговым методом и показывают, что высокоамплитудные сигналы АЭ регистрируются с более высокой точностью.
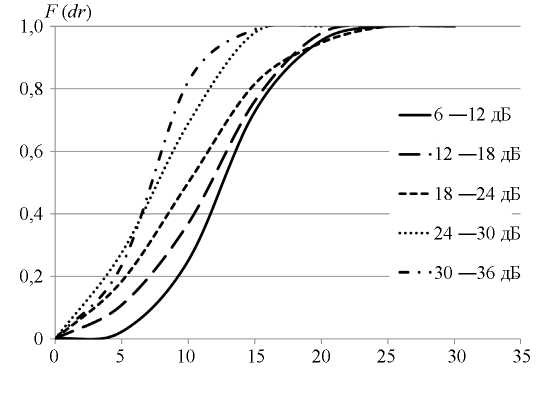
 для сигналов с различным уровнем их максимальной амплитуды! при определении времен прихода пороговым методом.
для сигналов с различным уровнем их максимальной амплитуды! при определении времен прихода пороговым методом.Причем приведенная зависимость вероятности определения координаты источника от величины относительной погрешности характерна во всех случаях при условиях разной чувствительности преобразователей, разной величины пьезоантенны, изменения величины порога чувствительности, местоположения источника в зоне контроля. Это наблюдалось при обработке данных от естественных источников.
Однако в [3, 4] проведены исследования, доказывающие, что точность оценки координат зависит от способа определения моментов времен прихода сигналов АЭ на приемные преобразователи. Поэтому на следующем этапе провели расчет времен прихода сигналов на преобразователи разными способами, кроме порогового еще использовали способ с плавающим порогом и двухинтервальный метод.
При анализе фиксированный порог устанавливали +26 дБ относительно среднеквадратического отклонения собственных шумов приемных преобразователей. Плавающий порог устанавливали 14 дБ относительно среднеквадратического отклонения уровня шумов в интервале 0,5 мс в соответствии с формулой
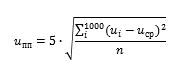
где п = 1000 — число обрабатываемых значений, полученных с дискретностью 0,5 мкс; и. — текущее значение амплитуды из п-го числа значений; иср — среднее значение амплитуды в интервале наблюдения.
При оценке времен прихода двухинтервальным методом значение времени определяли как момент, когда дисперсия значений амплитуды в интервале 32 мкс достигала 1/3 от максимального значения дисперсии сигнала в таком же интервале времени в окрестности максимума амплитуды. Значения параметров двухинтервального метода были установлены экспериментальным путем как имеющиенаименьшую погрешность при варьировании этих параметров для одних и тех же сигналов АЭ.
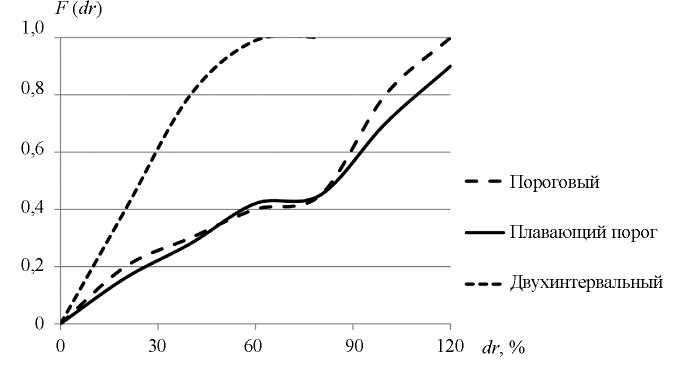
После определения времен прихода тремя разными способами (с фиксированным порогом, с плавающим порогом и двухинтервальным) сравнивали по тем же экспериментальным результатам вероятность определения координат с заданной погрешностью. Полученные результаты показали, что для сигналов с малой амплитудой на ближайшем к источнику приемнике (до 18 дБ относительно фиксированного порога) наиболее высокой вероятностью определить координаты с малой погрешностью обладает способ с плавающим порогом (рис. 4). Однако при повышении амплитуды принятого сигнала большей точностью определения координат обладают способы с фиксированным порогом и двухинтервальный, причем последний — с малой погрешностью.
Таким образом, в зависимости от уровня погрешности определения координат источников для конкретного объекта контроля или его отдельного участка можно определить способ определения времен прихода сигналов АЭ на приемники (в зависимости от максимальной амплитуды сигналов) для расчета координат. На следующем этапе исследований аналогичной обработке данных о сигналах АЭ и вероятностному анализу подвергли времена и скорости нарастания сигналов АЭ и их влияние на погрешность определения координат. Данные для вероятности определения координат с погрешностью для метода с плавающим порогом при времени нарастания сигнала в диапазоне 0 — 100 мкс приведены на рис. 5. Они показывают, что метод с плавающим порогом с относительно высокой
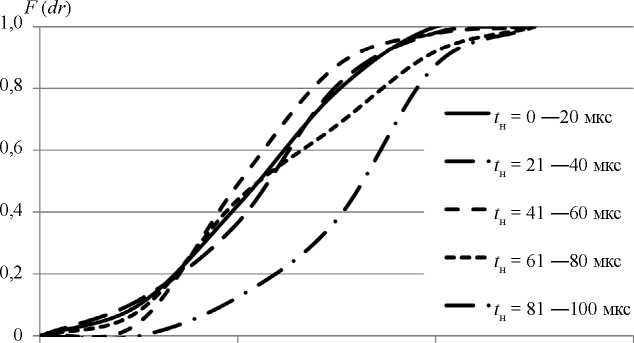
 для сигналов с различным временем нарастания сигналов при определении времен прихода методом с плавающим порогом.
для сигналов с различным временем нарастания сигналов при определении времен прихода методом с плавающим порогом.точностью определяет координаты источника в средней части пьезоантенны при времени нарастания сигналов на первый приемный датчик до 60 мкс, при повышении времени этот метод имеет высокую погрешность, как и пороговый. При увеличении времен нарастания сигналов свыше 100 мкс погрешность существенно возрастает и использование этих методов нецелесообразно. Для сигналов с большими временами нарастания относительно высокую вероятность достаточно точно определить местоположение источника имеет двухинтервальный метод. Результаты обработки сравнительных данных разными методами для сигналов с большими временами нарастания сигналов приведены на рис. 6.
Полученные результаты расчета вероятностей определения координат источника с заданной погрешностью можно свести в таблицы для каждого способа определения времен прихода сигналов. Пример рассчитанных значений вероятности быть локализованным с точностью не хуже 10 % в прямоугольной пьезоантенне, установленной на надрессорной балке, для способа с плавающим порогом приведен в таблице.
Таблица
Распределение вероятностей определения координат источника с погрешностью не более 10 % способом с плавающим порогом в зависимости от величины амплитуды и времени нарастания сигналов
| Диапазон времен нарастания сигнала, мкс | Диапазон амплитуд относительно порогового уровня, дБ | ||||
| 6—12 | 12—18 | 18—24 | 24—30 | 30—36 | |
| 0—20 | 0,38 | 0,4 | 0,5 | 0,5 | 0 |
| 21—40 | 0,22 | 0,5 | 0,67 | 0,4 | 0 |
| 41—60 | 0,14 | 0,3 | 0,42 | 0,5 | 0,57 |
| 61—80 | 0 | 0,41 | 0,57 | 0,5 | 0,75 |
| 80—100 | 0 | 0,33 | 0,5 | 0,5 | 0 |
| 100—120 | 0,11 | 0,2 | 0,5 | 0,5 | 0 |
Рассчитав таким образом вероятности для разных способов определения времен прихода сигналов АЭ, можно выделить наиболее надежный из них для заданных этих параметров для разных областей сигналов с заданной погрешностью определения координат. Картина наиболее достоверных способов определения координат источников АЭ на литой детали аналитически (с учетом координат приемников для погрешности не хуже 10 %) приведена на рис. 7. Полученное поле позволяет на основании зарегистрированных максимальной амплитуды сигналов АЭ и их времени нарастания определять наиболее достоверный способ оценки времен прихода.
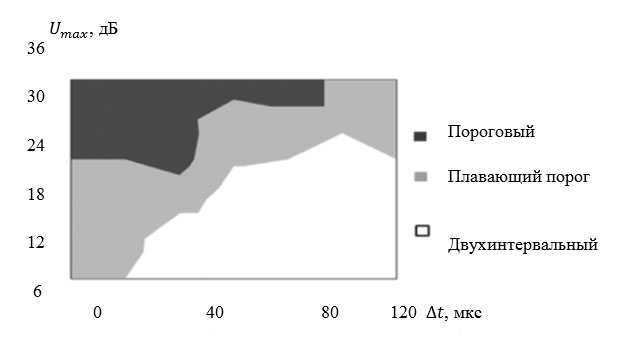
Проведенные исследования показывают, что в зависимости от собственных параметров сигналов АЭ, полученных в конкретной разновидности объекта, можно с заданной вероятностью определить значение погрешности определения координат источников. Также можно с заданной погрешностью определения координат источников АЭ давать вероятностную оценку этой погрешности. Кроме того, приведенная модель позволяет выбирать наиболее оптимальный способ определения времен прихода сигналов АЭ от одного акта на приемники с наиболее высокой вероятностной оценкой погрешности координат.
Данная методика оценки достоверности определения координат источника АЭ имеет перспективы в возможности привлечения других параметров сигналов для оценки уровня погрешности, а также способов определения исходных параметров для расчета координат источника — времен прихода сигналов АЭ на преобразователи, скорости распространения акустической волны и ее дисперсии.
ФГБОУ ВО «Сибирский государственный Поступила в редакцию
университет путей сообщения» 22 апреля 2014 г.
г. Новосибирск
ЛИТЕРАТУРА
- 1. Грешников В.А., Дробот Ю.Б. Акустическая эмиссия. Применение для испытаний материалов и изделий. — М.: Изд-во стандартов, 1976. — 272 с.
- 2. Серьезнов А.Н., Степанова Л.Н., Ивлиев В.В., Кабанов С.И., Бехер С.А., Власов К.В., Бобров А.Л., Кареев А.Е., Лебедев Е.Ю., Канифадин К.В., Рамазанов И.С., Тенитилов Е.С., Кочетков А. С. Акустико-эмиссионный контроль железнодорожных конструкций. — Новосибирск: Наука, 2011. — 272 с.
- 3. Муравьев В.В., Муравьев М.В., Бехер С. А. Применение новой методики обработки сигналов АЭ для повышения точности локализации дефектов. — Дефектоскопия, 2002, № 8, с. 53—65.
- 4. Бобров А.Л. Применение комплексного метода определения координат источников сигналов дискретной акустической эмиссии. — Тр. конф. «Фундаментальные проблемы формирования техногенной геосреды». — Новосибирск, 2009, т 2, с. 248—252.
- 5. Буденков Г.А., Недзвецкая О . В . Динамические задачи теории упругости в приложении к проблемам акустического контроля и диагностики. — М.: Изд-во физ.-мат. лит-ры, 2004. — 136 с.
- 6. Бобров А.Л., Сизова А. А. Анализ факторов, определяющих точность локализации источников сигналов дискретной акустической эмиссии. — Сб. тр. Всерос. науч.-практ. конф. «Качество и инновации — основа современных технологий». — Новосибирск: НГАСУ, 2010, с. 90—93.
- 7. Степанова Л.Н., Рамазанов И.С., Кабанов С.И., Лебедев Е.Ю. Локализация источников сигналов акустической эмиссии с учетом погрешностей измерения скорости звука и времени их прихода на датчики пьезоантенны. — Контроль. Диагностика, 2008, № 10, с. 60—64.

